This leaves our final option, which is to hold that a normatively-grounded approach to the granularity problem in causal modelling should allow for lossy compression, and that Woodward’s proportionality criterion should be modified to allow for this. As a guide to how this could go, there is some work in the philosophy of science and machine learning literature on coarse-graining and variable choice in causal models that explicitly allows for lossy compression in accordance with agential interests; see for instance Brodu (2011), Icard and Goodman (2015), Kinney (2019), Beckers, Eberhardt and Halpern (2019), and Kinney and Watson (2020). Each of these approaches use utility functions or stipulate an acceptable level of information loss when coarse-graining causal variables in order to arrive at a tractable causal model of some system of interest.
To illustrate, suppose that we knew that if a patient smoked 20 Marlboro cigarettes a day for ten years, then their probability of developing lung cancer was slightly higher than if they smoked 20 cigarettes of some other brand every day for the same time period. Under these conditions, the more proportional causal variable for an agent who cares about preventing lung cancer would be one that distinguishes between these two types of cigarette brands. But one can easily imagine an agent who says, despite the difference that brand makes to one’s probability of lung cancer, that no matter what, if one wants to avoid lung cancer, then one simply should not smoke. That is, for the sake of manipulation and control, they don’t care enough about the differences between cigarette brands to account for this difference when building a causal model of their environment. By Woodward’s own standards, such an agent would favor a binary causal variable with the values {smoker, non-smoker}, even though this is not consistent with Woodward’s proportionality criterion for variable choice, since it amounts to a case of lossy compression.
where V has the possible values {v, ~v}, and where e is either of the two values of E (p. 377). Here too, Woodward is effectively recommending against lossy compression, as this quantity measures how informative interventions on V are with respect to the value of E.
References
Walker, C. M., Lombrozo, T., Williams, J. J., Rafferty, A. N., & Gopnik, A. (2017). Explaining constrains causal learning in childhood. Child development, 88(1), 229-246.
Blanchard, T., Murray, D., & Lombrozo, T. (2021). Experiments on causal exclusion. Mind & Language.
In Chapter 1 of Causation with a Human Face, James Woodward articulates the metaphilosophical outlook on causation that gives his book its title. He tells us that his aim is to articulate a normative theory about how human beings ought to engage in causal reasoning. However, he believes that when building such a theory, one must also account for empirical data describing how human beings actually reason about causation. The human mind, he argues, is finely-tuned by millennia of evolution and years of learning, such that data showing how we actually reason about causation should serve as a good guide to how to be an effective causal reasoner, and hence to how we ought to reason about causation. In the background is a metaphilosophy according to which the sole good-making feature of an account of causal reasoning is its usefulness in helping human beings achieve their goals as agents. That is, our actual goals as agents define a functional standard according to which we assess normative accounts of causal reasoning.
We hope that this piece will be read mostly as an invitation (to both Woodward and other philosophers and psychologists) to say more about how humans coarse-grain their implicit causal models of their environment, and how this coarse-graining reflects agential goals. This process of coarse-graining is central to how we understand our environment (i.e., how we form what Sellars (1963) called our “manifest image” of the world) in a way that allows for systematic and robust causal inference. Thus, we take coarse-graining to be a crucial part of the conceptual link between human psychology and the theory and practice of science. And it is the investigation of just this conceptual link that forms the core of Woodward’s project, both in this book and throughout his rich catalogue.
[3] It is worth noting that there is some indirect evidence that people might engage in lossy compression when pursuing causal reasoning. For instance, there is evidence that in estimating the probability of an effect given a cause, people operate with a causal model that is lossy in the sense that it omits alternative causes (Fernbach, Darlow, & Sloman, 2010, 2011). In choosing between two causal hypotheses, children sometimes favor the cause consistent with prior beliefs over the cause that better fits their observations, thus tolerating a loss in fidelity (Walker et al., 2017). For token-level causal claims, people sometimes favor claims at higher-levels over those that are maximally specific (Blanchard, Murray, & Lombrozo, 2021), and favor explanations that cite higher-level generalizations (Johnston et al., 2018) or match the level of the explanandum (Johnson & Keil, 2014). In Williams et al. (2013), participants who are prompted to explain why category members belong to their categories, more so than those in control conditions, rely on something like a single causal variable that explains most (but not all) cases vs. on an ugly disjunction that explains all cases. Finally, in Ho et al. (2021), participants who attempted to navigate an environment in order to achieve the goal of reaching an endpoint while avoiding obstacles were found to elide goal-irrelevant details in their representation of that environment. The authors of this study adopt an explicitly causal understanding of what counts as both a goal and an obstacle. This is not an exhaustive list of the evidence, but to our knowledge no prior work has directly investigated whether people exhibit lossy compression in solving the grain problem for type-level causal hypotheses or explanations.
What about when the dynamics governing the system of interest are not deterministic? Woodward has far less to say about this case than the deterministic one, even though his theory of causation is intended primarily as an analysis of statistical causal claims such as “smoking causes lung cancer.” When the causal variable V and effect variable E are both binary, we can make a proportionate choice of causal variable by choosing the variable that maximizes the following quantity:
where E has n total values and V has m total values.[2] If we take this measure on board, then once again it seems that the proportionality criterion recommends against lossy compression, since proportionality is formalized as the average amount of information that interventions on the causal variable transmit about the value of the effect variable.
Icard, T., & Goodman, N. D. (2015, July). A Resource-Rational Approach to the Causal Frame Problem. In CogSci.
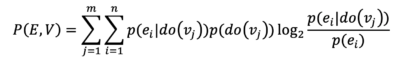
Kinney, D., & Watson, D. (2020, February). Causal feature learning for utility-maximizing agents. In International Conference on Probabilistic Graphical Models (pp. 257-268). PMLR.
Sellars, Wilfrid (ed.) (1963). Science, Perception and Reality. New York: Humanities Press.
The place to look for an answer to this question is in Chapter 8, where Woodward discusses his principle of proportionality. For Woodward, proportionality is the criterion that humans should use when they choose the optimal level of granularity for a causal variable, given some effect. To briefly summarize what is presented with a high degree of technicality in the chapter, for a given effect variable E, the choice of causal variable V from a set of alternatives V is proportional to the extent that, ceteris paribus, the variable V “correctly represents more rather than fewer of the dependency relations concerning the effect or explanandum that are present, up to the point at which we have specified dependency relations governing all possible values of E” (p. 372). Importantly, the alternatives V should be understood as all representing the same type of phenomenon at different levels of granularity (e.g., smoking cigarettes, smoking high-tar cigarettes, smoking high-tar Marlboro cigarettes, etc…).
Beckers, S., Eberhardt, F., & Halpern, J. Y. (2020, August). Approximate Causal Abstractions. In Uncertainty in Artificial Intelligence (pp. 606-615). PMLR.
There is some evidence that Woodward wants to resist approaches like these. He writes that proportionality is a “pragmatic virtue in the sense that it has a means/ends rationale or justification, [but] it is not ‘pragmatic’ in the sense that it depends on the idiosyncrasies of particular people’s interests or other similarly ‘subjective’ factors” (p. 373). This suggests that if Woodward’s proportionality criterion is to be amended to allow for lossy compression, then the amount of loss that is to be tolerated will have to be fixed not by the contextual conditions of a given agent’s motivations for engaging in causal reasoning, but rather by some more universal or objective determinant of what counts as acceptable information loss. There are reasons for skepticism that such a sharp contrast between subjective and objective determinants of tolerable information loss can be drawn. Even in stock examples like the causal generalization “smoking causes lung cancer,” the value of the generalization derives from a subjective concern with preventing cancer that may not be universally shared.
Ho, M. K., Abel, D., Correa, C. G., Littman, M. L., Cohen, J. D., & Griffiths, T. L. (2021). Control of mental representations in human planning. arXiv preprint arXiv:2105.06948
Johnston, A. M., Sheskin, M., Johnson, S. G., & Keil, F. C. (2018). Preferences for explanation generality develop early in biology but not physics. Child Development, 89(4), 1110-1119.
Kinney, D. (2019). On the explanatory depth and pragmatic value of coarse-grained, probabilistic, causal explanations. Philosophy of Science, 86(1), 145-167.
When the dynamics of the system under study are such that each variable in the set V is deterministically related to E, applying the proportionality criterion is straightforward. We select the variable V which, to the greatest extent possible, allows us to intervene on V so as to induce E to take any of its values. To illustrate, if E is a variable denoting whether a lightbulb is on or off, and there is a light switch that perfectly determines whether the lightbulb is on or off, then a maximally proportionate choice of causal variable V would be a binary variable denoting whether the switch is in the on or off position. Importantly, if there were also a dial with ten positions, five of which ensured that the bulb was on and five of which ensured that the bulb was off, then a choice of causal variable V denoting the position of this dial would also be a maximally proportional choice with respect to E. Even though there is some redundancy in the system, both variables allow for maximal control over whether the lightbulb is on or off.[1]
Brodu, N. (2011). Reconstruction of epsilon-machines in predictive frameworks and decisional states. Advances in Complex Systems, 14(05), 761-794.
Williams, J. J., Lombrozo, T., & Rehder, B. (2013). The hazards of explanation: Overgeneralization in the face of exceptions. Journal of Experimental Psychology: General, 142(4), 1006.
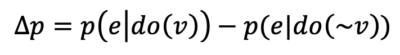
[2] Note here that while Pocheville et al.’s proposed measure of proportionality contains the term p(do(vj)), strictly speaking this term is not well-defined according to the standard theory of causal Bayesian networks. However, using “intervention variables” (see Pearl 1994), one can augment the causal Bayes nets framework so that this term is well-defined.
Pocheville, A., Griffiths, P. E., & Stotz, K. (2017, August). Comparing causes—an information-theoretic approach to specificity, proportionality and stability. In Proceedings of the 15th congress of logic, methodology and philosophy of science (pp. 93-102). London: College Publications.
Fernbach, P. M., Darlow, A., & Sloman, S. A. (2010). Neglect of alternative causes in predictive but not diagnostic reasoning. Psychological Science, 21(3), 329-336.
Third, one could argue that humans do not, in fact, engage in lossy compression as part of causal reasoning. Given Woodward’s comments in this book, there is no indication that he would take this route, and, for our part, it does not seem especially plausible. But we also note that there are, to our knowledge, no empirical studies directly testing whether people engage in lossy compression when formulating type-level causal hypotheses or explanations.[3] This suggests an intriguing line of future research for cognitive science and experimental philosophy.
Fernbach, P. M., Darlow, A., & Sloman, S. A. (2011). Asymmetries in predictive and diagnostic reasoning. Journal of Experimental Psychology: General, 140(2), 168.
Let us begin by pursuing the first route. For Woodward, the reason why we ought to prefer proportional causal models is straightforward: proportional models identify “the level [of causal description] that is most informative about the conditions under which the effect will and will not occur” (p. 389). But this just invites the further question of what it is about the informativeness of a cause with respect to its effect that is valuable to human agents. Woodward’s answer here is that an informative causal relationship is valuable because it does “a better job at providing information that is associated with such distinctive aims of causal thinking as manipulation and control” (p. 373). While enhanced manipulation and control of the value of some variables is certainly desirable for human agents in many contexts, these desiderata can be traded off against other agential interests. Moreover, given agential interests, there may be increases in the informativeness of a cause with respect to its effect that have no value to an agent.
Note that this application of the proportionality criterion vitiates against lossy compression. When we engage in lossy compression, we arrive at a coarse-grained causal model of some system by tolerating some reduction in the amount of information that can be passed between cause and effect, compared to a more fine-grained representation of the same system.
As Woodward himself puts it, “it is a striking empirical fact that the difference-making features cited in many lower-level theories sometimes can […] be absorbed into variables that figure in upper-level theories without a significant loss of difference-making information with respect to many of the effects explained by those upper-level theories” (emphasis ours) (p. 383). This suggests that insignificant difference-making information can be elided from our causal model of some system of interest. Indeed, this is exactly what happens in cases of lossy compression: a certain amount of information about difference-making relationships is judged to be insignificant when we represent the causal dynamics of our environment.
Pearl, J. (1994, July). A probabilistic calculus of actions. In Proceedings of the Tenth international conference on Uncertainty in artificial intelligence (pp. 454-462).
To make this more concrete, consider the analysis offered in Kinney (2019). Imagine an expected-utility maximizing agent with a utility function defined over all pairs consisting of an action from a set A and a value of an effect variable E. Given the relationship between a causal variable C and its effect E, we can ask such an agent how much they would be willing to pay to learn which intervention had been performed on C, before they choose an action from A. Suppose that there is some coarsening C¢ of C such that there isgreater proportionality between C and E (by the lights of Pocheville et al.’s measure) than there is between C¢ and C. That is, the choice of C¢ over C amounts to an instance of lossy compression. Nevertheless, there are scenarios in which such an agent would pay no more to learn which interventions had been performed on C than they would pay to learn which interventions has been performed on C¢. For instance, an agent concerned with preventing lung cancer might pay just as much to learn about interventions such that a patient either smokes or does not as she would to learn about interventions in which the brand of cigarettes smoked is specified, even when some cigarettes are more carcinogenic than others. In these cases, it seems that this agent has a clear pragmatic justification for engaging in lossy compression, even though this goes against the recommendation of proportionality, and even though it seems to depend on the kinds of personal idiosyncrasies that Woodward wants to avoid when formulating his own solution to the grain problem.
The grain problem concerns how we choose an appropriate level of granularity for the variables that we use in our causal models of the world. We posit that human beings often choose to represent the causal structure of the world using coarse-grained generalizations such as “smoking causes lung cancer,” rather than more fine-grained generalizations such as “smoking at least 100,000 high-tar cigarettes over the course of twenty years causes lung cancer.” Choosing the former generalization over the latter often involves a process of lossy compression. Even though the latter generalization allows for the representation of more dependencies between cause and effect than the former, we choose the former, more compressed generalization, plausibly due to its simplicity, tractability, or generalizability.
If we pursue the second route, and aim to find an alternative desideratum for a causal model that is satisfied at the expense of proportionality in cases of lossy compression, a natural candidate is simplicity. Compressed models are simpler models, in the sense that they use variables with fewer values. In cases of lossy compression, we may want to say that the loss in difference-making information between cause and effect diminishes the proportionality of the causal representation, but increases its simplicity, achieving an optimal balance. This is plausible, but there are indications that it is not the move Woodward would make. This kind of simplicity, he writes, is best understood as “descriptive simplicity,” which he contrasts with “the kind of simplicity that is supposedly relevant to choosing among different empirical alternatives” (p. 382, footnote 37). This suggests that Woodward does not take merely descriptive simplicity to be a genuine desideratum for causal representations, such that this option is not one he wishes to take.
[1] In this respect, Woodward’s definition of proportionality revises (correctly, in our view) the definition of proportionality given in Woodward (2010), which held that maximally proportional causal relationships were characterized by a one-to-one function between the causal variable and the effect variable.
We find ourselves at a juncture. On the one hand, we posit that humans do engage in lossy compression when representing the causal structure of their environment, and some of Woodward’s comments in this book seem to agree with this posit (e.g., his comment, quoted above, on the ability of higher-level theories to retain significant information from lower-level theories). Moreover, Woodward is clear that he takes the actual cognitive practices of human beings to provide relevant data for constructing a normative theory of causation. Taken together, these two claims appear to be in tension with the recommendation against lossy compression that is implicit in Woodward’s account of proportionality. Thus, it seems that we will have to either: i) say something about why, in this instance, the practice of lossy compression by actual agents is not a good guide to a normative theory of causal proportionality, ii) identify a different good-making feature of a causal explanation that is traded off with proportionality in cases of lossy compression, iii) argue that in fact, humans do not engage in lossy compression as part of causal reasoning, or iv) amend the account of proportionality to allow for lossy compression.
Woodward, J. (2010). Causation in biology: stability, specificity, and the choice of levels of explanation. Biology & Philosophy, 25(3), 287-318.
The question we set out to answer here is the following: are there cases in which the normative theory of causal reasoning laid out in Woodward’s book recommends lossy compression when choosing causal variables?
We believe that Woodward is correct with respect to what a theory of causation and causal reasoning ought to do. What we want to explore in this post is the normative issue of how we ought to choose causal variables for use in descriptive and explanatory reasoning, with a particular focus on the “grain problem” in causal reasoning.