One of Woodward’s most important contributions to the study of causation is his introduction of the notion of invariance across background conditions. Woodward‘s ideas on this topic have had a major influence on experimental research in causal cognition (including on my own work), and I thought it might be helpful to do a little bit to help bring out the importance of this contribution.
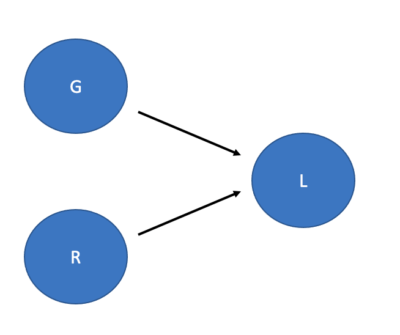
P(G) = .5
Most importantly for present purposes, people’s probability of thinking about a possibility seems to be shaped by their value judgments. If you think that a certain possibility is good or right, you will be more inclined to think of that possibility, even controlling for the degree to which you believe that there is a high probability that it will actually be realized. Thus, in our own work, we find that the probability of thinking about a given possibility x is approximately proportional to F(x)e^(V(x)/t), where F(x) is the person’s belief about how frequent x is, V(x) is the person’s belief about how valuable x would be, and t is a temperature parameter.
First off, what exactly is invariance across background conditions? Perhaps the easiest way to convey the basic idea is to introduce a simple example. Suppose that Samantha lives in a deeply racist society. In this society, if you have dark skin, people will deny you educational opportunities, and you will therefore be illiterate. Samantha has certain genes that give her dark skin, so she is denied educational opportunities, and she becomes illiterate.
But now it seems that we face a further question. When people are thinking about the causal connection between two variables, they couldn’t possibly think about invariance across all possible background variables. They have to think about some variables and not others. So then, in people‘s ordinary causal cognition, which particular variables do people consider when they are checking for invariance across background conditions?
The cognitive processes here, I have been suggesting, cannot be explained just in terms of the probabilities people assign to values of the background variables. Instead, they are fundamentally bound up with the value judgments people make about values of the background variables.
With all that in mind, let’s consider again how to apply Woodward‘s theory of invariance across background conditions to the case of a person growing up in a racist society. You might believe that it is extremely improbable that the society would not be racist, but all the same, you might believe that it would be deeply valuable for the society to not be racist. For this reason, despite your beliefs about the probabilities, you will be drawn to think about possibilities in which the society is not racist. The result is that when you are considering the connection between G and L, you will be drawn to ask whether it would still hold in possibilities in which R = 0. Since it does not, you will be inclined to think that Samantha’s genes are not genuinely the cause of her illiteracy.
Now, one natural hypothesis would be that if people think that this is the way the world actually works, they will be relatively unconcerned about whether the causal connection is invariant across that particular background variable. This hypothesis might sound plausible in theory, but actual empirical studies consistently find that things actually don’t work like that at all. Instead, it seems that we need to be thinking about a different sort of probability. We need to be thinking about probabilities of people thinking about possibilities. This is not just the same thing as the sort of probability discussed above. In certain cases, people believe that a certain possibility is extremely improbable, but all the same, there’s a very high probability that people will think of that possibility.
P(L | R, G) = .9 – .85RG
In this example, we are assuming that people think it is extremely improbable that the society has no racism. In other words, it is true that Samantha’s genes would have no impact on her literacy if society were not racist, but it is extremely improbable that society would not be racist, so the probability that we would be in a situation in which the causal connection between these two variables did not hold is extremely low.
One obvious initial hypothesis would be that the answer follows naturally from people‘s beliefs about the probability of possibilities. For example, suppose that people represent the example we’ve been discussing here using a Bayes net, as follows:
Suppose we now consider two different variables: Samantha’s genes (G) and her literacy (L). What we find is that, given the precise way that things are set up in the actual world, there is indeed a connection between these variables: an intervention on G will lead to a change in L. However, suppose we now consider a third variable: the presence of racism in the society (R). Then we can say that the connection between G and L is not invariant over R. There just happens to be a connection between Samantha’s genes and her literacy in the actual world because of the presence of racism, but if there weren’t any racism, there wouldn’t be any connection between these two variables. Woodward’s introduction of this concept has done a tremendous amount to shape contemporary research in causal cognition, and at this point, I think it’s fair to say that we have very strong evidence that people do indeed engage in a cognitive process that involves checking for invariance across background conditions.
P(R) = .99


